Um tanque torisférico é um tipo de tanque de armazenamento ou reservatório que possui uma forma esférica combinada com uma seção toroidal. Ele é uma combinação de uma semiesfera (meia esfera) e um toro (anel).
Esse design é escolhido para certas aplicações devido às suas propriedades específicas. O formato torisférico oferece uma combinação de resistência estrutural e eficiência de armazenamento. A seção esférica proporciona uma distribuição uniforme de tensões e pressões internas, enquanto a seção toroidal maximiza a capacidade de armazenamento em relação a um tanque esférico padrão.
O tanque torisférico é frequentemente utilizado em aplicações que envolvem armazenamento de líquidos ou gases pressurizados, como tanques de gás, tanques de armazenamento de produtos químicos ou tanques de armazenamento de combustível. A forma torisférica permite uma distribuição eficiente do material armazenado, minimizando o espaço vazio e aproveitando ao máximo a capacidade de armazenamento do tanque.
Os tanques torisféricos são construídos com materiais resistentes à corrosão, como aço carbono ou aço inoxidável, dependendo da natureza do material armazenado. Eles são projetados levando em consideração fatores como a pressão interna, a capacidade de armazenamento, as condições de operação e os requisitos de segurança aplicáveis.
Esses tanques podem ser dimensionados em diferentes capacidades, desde pequenos tanques para uso residencial até grandes tanques industriais. Eles são fabricados com soldas e reforços estruturais adequados para garantir a integridade e a segurança do tanque.
Os tanques torisféricos oferecem vantagens em termos de resistência estrutural, eficiência de armazenamento e distribuição de tensões. Eles são amplamente utilizados em várias indústrias onde é necessário armazenar líquidos ou gases pressurizados de forma segura e eficiente.
Calculadora de Volume e Peso de Tanque Torisférico
Instruções:
1 - Insira valor de diâmetro e comprimento do costado em milímetros.
2 - Os valores de Raio da Coroa (Rc) e Raio nuckle (Rk) são fixados na condição mais crítica,
seguindo a ASME Seção VIII, Divisão I: RC=D e Rk=6%D, respectivamente.
3 - Insira os valores de espessura de Tampo e do Costado.
4 - Escolha calcular peso e volume considerando apenas um ou dois tampos.
5 - Escolha material de construção do tanque e o produto a ser contido, ambos para fins de cálculo de peso.
| Dimensões do tanque | Dados do tanque | Desenho do tanque | |||
|---|---|---|---|---|---|
| Diam. "D" (mm): | Rc-Rk : | 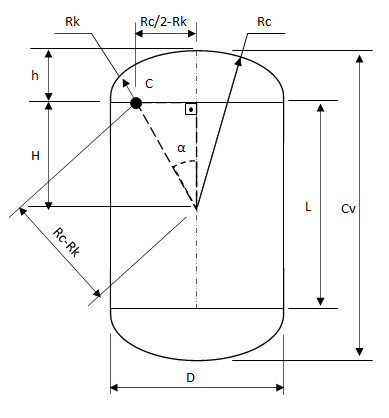 |
|||
| Costado "L"(mm): | (Rc/2)-Rk : | ||||
| Rc = D : | Altura "H" : | ||||
| Rk knuckle (6%D) : | Altura "h" : | ||||
| Espessura. Tampo (mm): | Altura "Cv" : | ||||
| Espessura Costado (mm): | Seno (α) : | Ângulo α : | |||
| Tampo Duplo: | Área Tampo : | Área Costado : | |||
| Material do Vaso: | Volume Tampo: | Volume Costado: | |||
| Produto: | Peso do Tampo : | Peso do Costado : | |||
| Peso TQ Vazio: | Peso TQ Cheio: | ||||
Revisão da Literatura
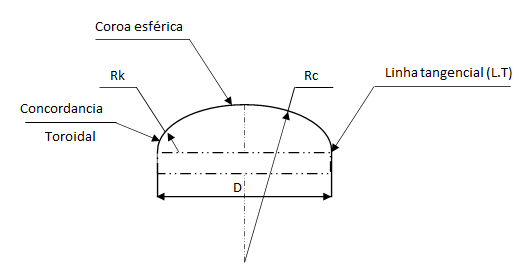
Segundo Silva Telles (2007), Os tampos torisféricos (Fig. 2.2(b)) são constituídos por uma calota central esférica (crown), de raio Rc. e por uma seção toroidal de concordância (knuckle), de raio Rk. O tampo torisférico é bem mais fácil de fabricar do que o elíptico, e essa facilidade é tanto maior quanto menos profundo for, isto é, quanto menor for o raio Rk. Inversamente, a sua resistência será tanto maior quanto maior for Rk, permitindo chapas de menor espessura. Qualquer tampo torisférico é sempre mais fraco do que um elíptico de mesmo diâmetro e com mesma relação de semieixos.
Ainda segundo Telles, O código ASME. Seção VIII,' Divisão I (parágrafo UG-32) e Divisão 2 (parágrafo AD-204), exige para os tampos torisféricos que o raio Rk Seja no mínimo 6% do diâmetro (segundo a norma ingles BS5500: 10%), ou 3 vezes a espessura da chapa — o que for maior -, e que o raio Rc seja no máximo igual ao diâmetro externo do tampo. Os tampos torisféricos com esses valores limites, isto é, Rk = 0.06 D e Rc = D, são os menos resistentes de todos ao efeito da pressão interna, exigindo por isso maior espessura de chapa. Qualquer tampo torisférico é tanto mais resistente quanto mais o seu perfil se aproxima de uma elipse perfeita. De todos os perfis torisféricos com relação de semieixos 2:1, o perfil em que se tem Rk = 0.1727 D e Rc = 0.9045 D (ou seja, Rk/Rc = 0.1909) é o que mais se aproxima da elipse. Esse perfil é conhecido como "falsa elipse", ou também como -"perfil Foggles"; é o mais empregado de todos os perfis torisféricos, e frequentemente confundido com o tampo elíptico verdadeiro. O tampo torisférico 'falsa elipse" de acordo com o código ASME. Seção VIII pode ser considerado equivalente ao tampo elíptico.
Para fazermos o traçado do tanque torisférico precisamos deduzi-lo geometricamente, para determinar, principalmente: A altura "H" do centro do raio da coroa até a linha tangencial; A altura "h" da linha tangencial "L.T" até o topo da coroa esférica; E o angulo "α" formado entre a linha de centro do tanque/ calota central e a linha que vai do centro do raio da coroa esférica até o ponto tangencial entre o raio toroidal "Rk" e o raio da coroa "Rc", que passa pelo centro "C" da concordancia toroidal.
Apesar de não estarmos tratando aqui dos cálculos de espessura e tensão máxima de trabalho admissivel, vale ressaltar que, aqui no Brasil os fabricantes/ construtoras, trabalham com raio toroidal (ou raio de rebordo) padronizado ou limitado, de 6% a 10%. Valores abaixo ou acima disso podem ser caracterizados especiais e demandar maior especificidade nos calculos de elementos finitos. Para mais informações selecionei aqui duas fontes: METAL TAMPOS e a ENSUS
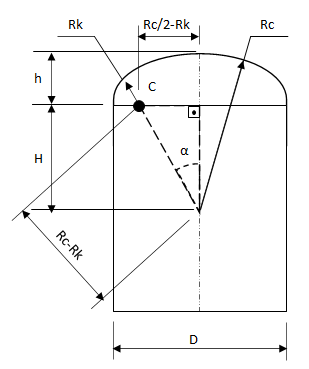
$$ \text{Raio da Coroa / Esfera Central: }R_c = D $$ $$ \text{Raio Toroidal (Knuckle) : }R_k = 0.06 \cdot D -à- 0.10 \cdot R_c $$ $$ \text{Seno do ângulo α: }sin(α) =\frac {(\frac{R_c}{2} - R_k)}{(R_c-R_k)} $$ $$ \text{Ângulo α: }α = arcsin(sin(α)) $$ $$ \text{Altura H: }H =cos(α) \cdot (R_c-R_k) $$ $$ \text{Altura h: }h =(R_c-H) $$
Depois de determinar as principais dimensões do tampo torisférico, podemos calcular o seu volume.
Aqui vamos denominar a altura da coroa "hc" da base formada pelo diametro D' até o topo da coroa, e a altura do perfil toroidal "hk", com base diametral igual a D e topo diametro igual a D', formados assim pelo segmento de esfera com o cilindro inscrito no perfil do segmento de esfera do toroide:

O volume do Tampo "Vt" é igual a soma do Volume da Coroa "Vc" mais o Volume da seção Toroidal "Vk". $$ \text{Volume do Tampo: }V_t = V_c + V_k $$
Primeiro calculamos o volume da Coroa com diametro de base D':
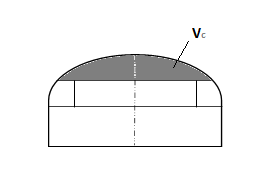
Em seguida, para calcular o volume da seção toroidal "Vk", calculamos o volume Vk1 do seguimento de esfera que contém o raio toroidal e adicionamos o volume Vk2 do cilindro inscrito no seguimento, e assim calculamos o volume da seção toroidal com diâmetro de base D e diametro de topo D':

Agora que temos o Volume do Tampo, adicionamos o Volume do Costado Vcostado para obter o Volume do Vaso . Aqui vamos considerar que o vaso possui os dois lados com tampo toriférico:

Referências Bibliográficas:
TELLLES, Pedro C. Silva. Vasos de Pressão: Cálculo e Projeto. 2ª ed. São Paulo: Blucher, 2007.
WOLFRAM. Sphere CAP. Disponível em:
https://mathworld.wolfram.com/SphericalCap.html. Acesso em: 02 de abril de 2023.
WOLFRAM. Spherical Segment. Disponível em:
https://mathworld.wolfram.com/SphericalSegment.html. Acesso em: 02 de abril de 2023.
WOLFRAM. Surface Revolution. Disponível em:
https://mathworld.wolfram.com/SurfaceofRevolution.html. Acesso em: 02 de abril de 2023.
OMNICALCULATOR. Sphere Volume Calculator. Disponível em:
https://www.omnicalculator.com/math/sphere-volume. Acesso em: 02 de abril de 2023.




